Cohesion and Repulsion in Bayesian Distance Clustering
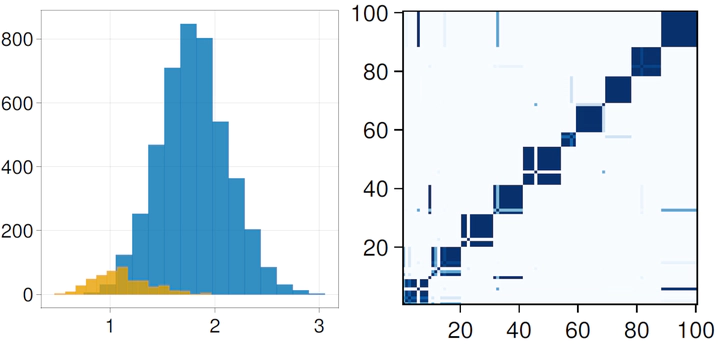 Inter/intra-cluster pairwise dissimilarities and posterior coclustering probabilities
Inter/intra-cluster pairwise dissimilarities and posterior coclustering probabilitiesAbstract
Clustering in high-dimensions poses many statistical challenges. While traditional distance-based clustering methods are computationally feasible, they lack probabilistic interpretation and rely on heuristics for estimation of the number of clusters. On the other hand, probabilistic model-based clustering techniques often fail to scale and devising algorithms that are able to effectively explore the posterior space is an open problem. Based on recent developments in Bayesian distance-based clustering, we propose a hybrid solution that entails defining a likelihood on pairwise distances between observations. The novelty of the approach consists in including both cohesion and repulsion terms in the likelihood, which allows for cluster identifiability. This implies that clusters are composed of objects which have small “dissimilarities” among themselves (cohesion) and similar dissimilarities to observations in other clusters (repulsion). We show how this modelling strategy has interesting connection with existing proposals in the literature as well as a decision-theoretic interpretation. The proposed method is computationally efficient and applicable to a wide variety of scenarios. We demonstrate the approach in a simulation study and an application in digital numismatics.