Chromatic Alpha Complexes
Theory and Applications
Abhinav Natarajan, Thomas Chaplin, Adam Brown, and Maria Jose Jiminez Rodriguez
Motivation from Spatial Biology
Data from patients: tissue slices of adenoma and carcinoma tissue.
Each sample is a record of the positions of different cell types within a tissue slice.
Primarily dealing with epithelial and immune cells.
Our aim: to quantify spatial interactions that correspond with clinical outcomes, and aid in qualitative analysis of tumour-immune microenvironment.
Spatial relationships
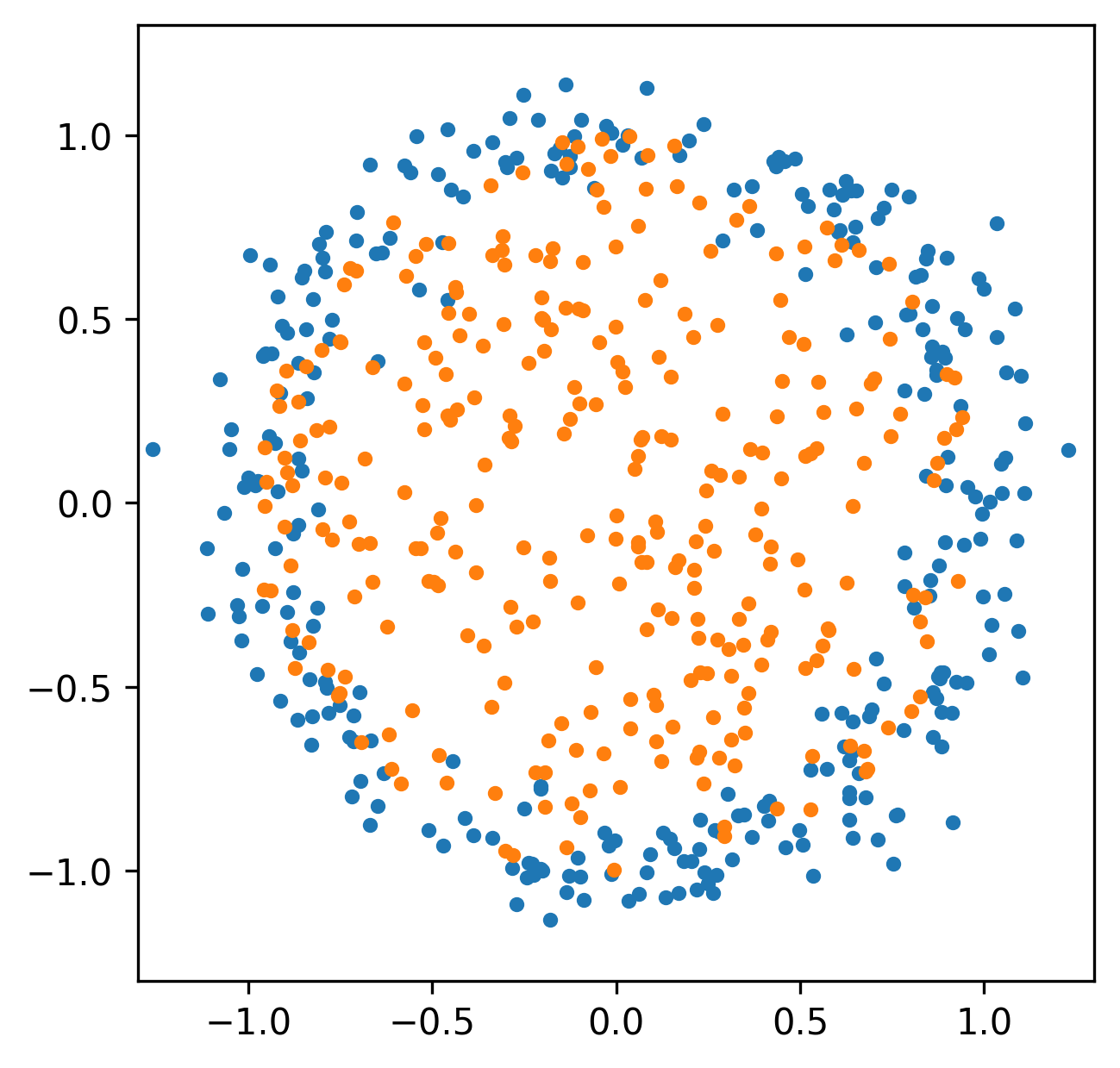
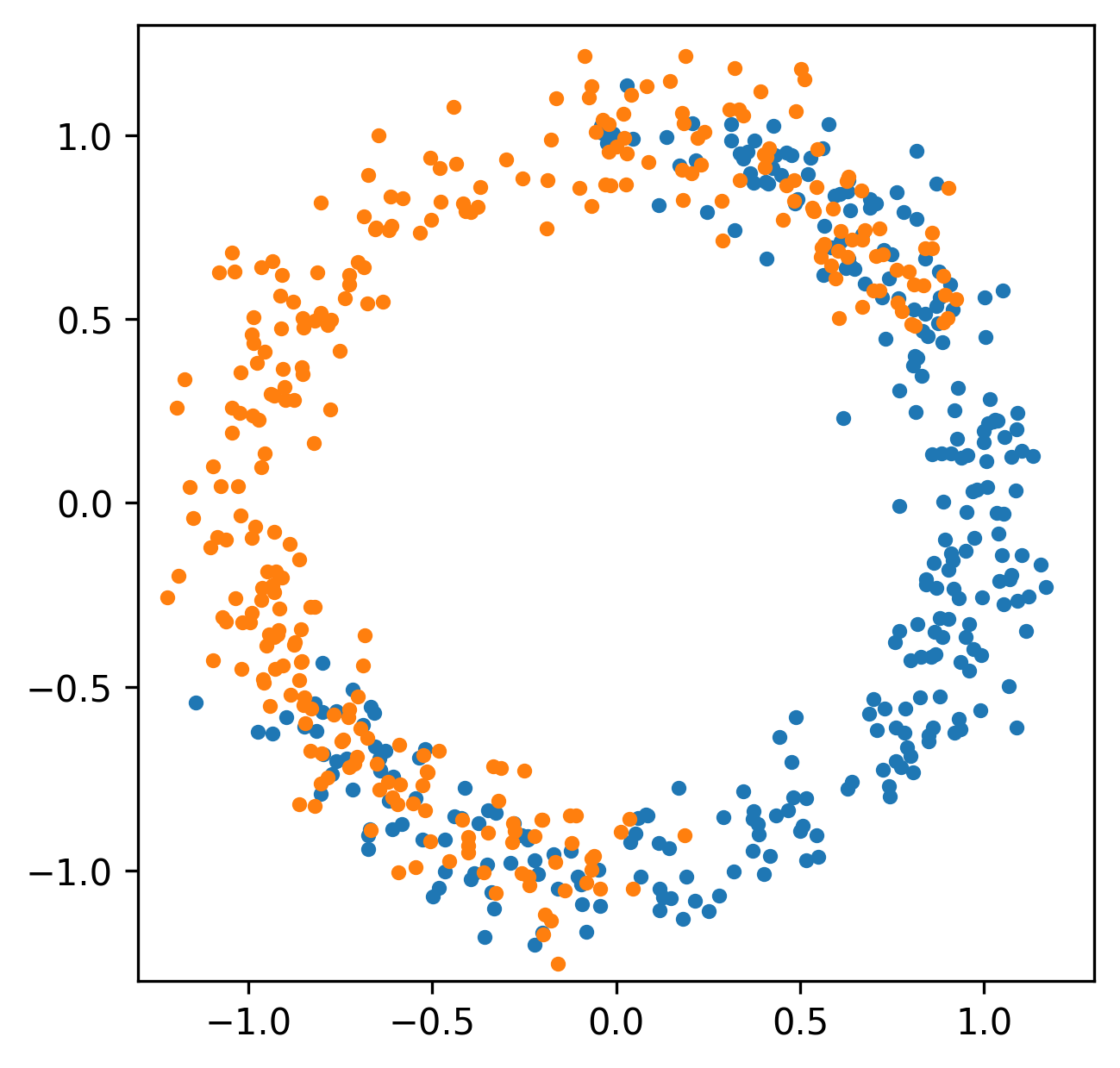
Funtoriality of Persistent Homology
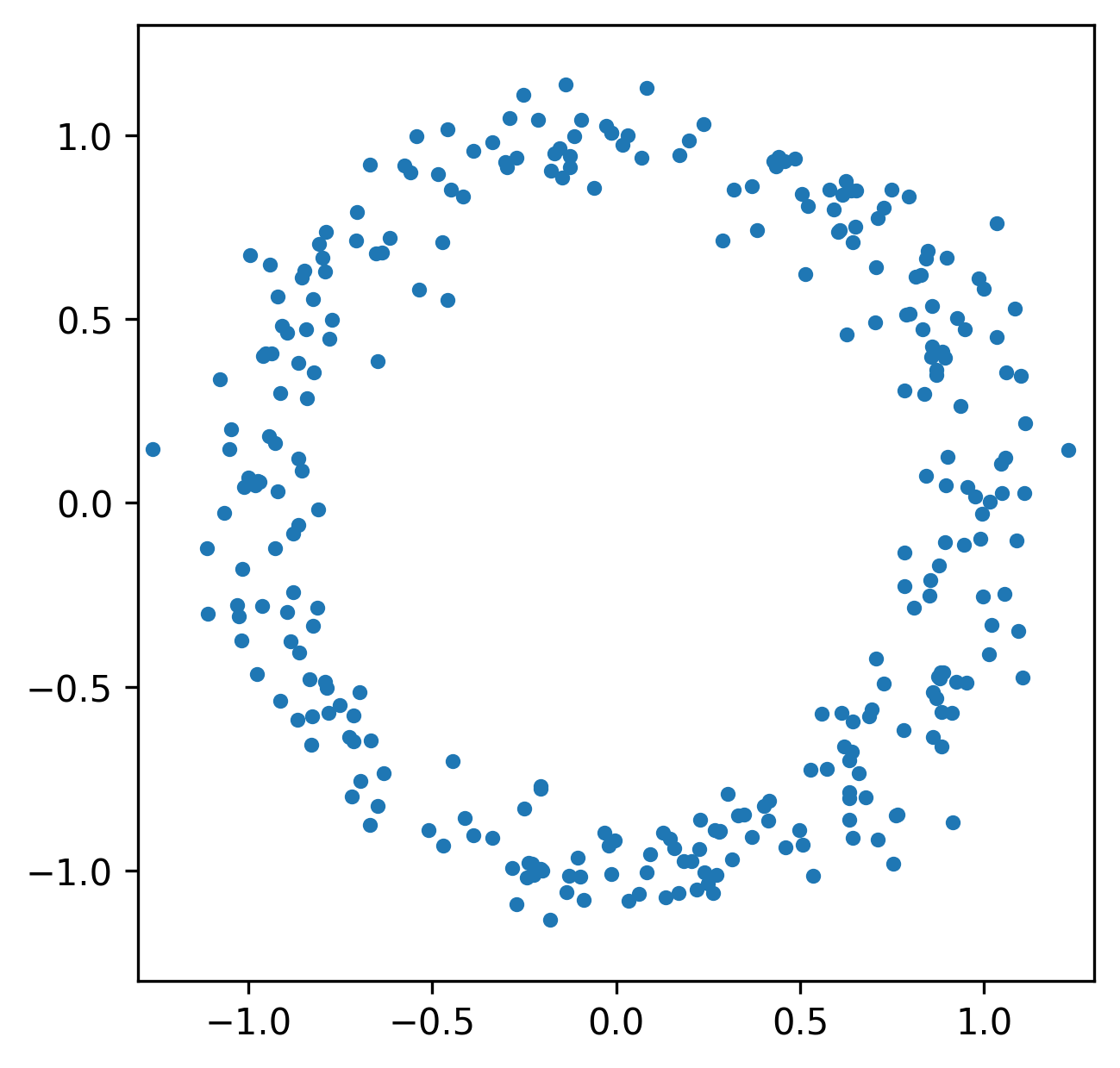
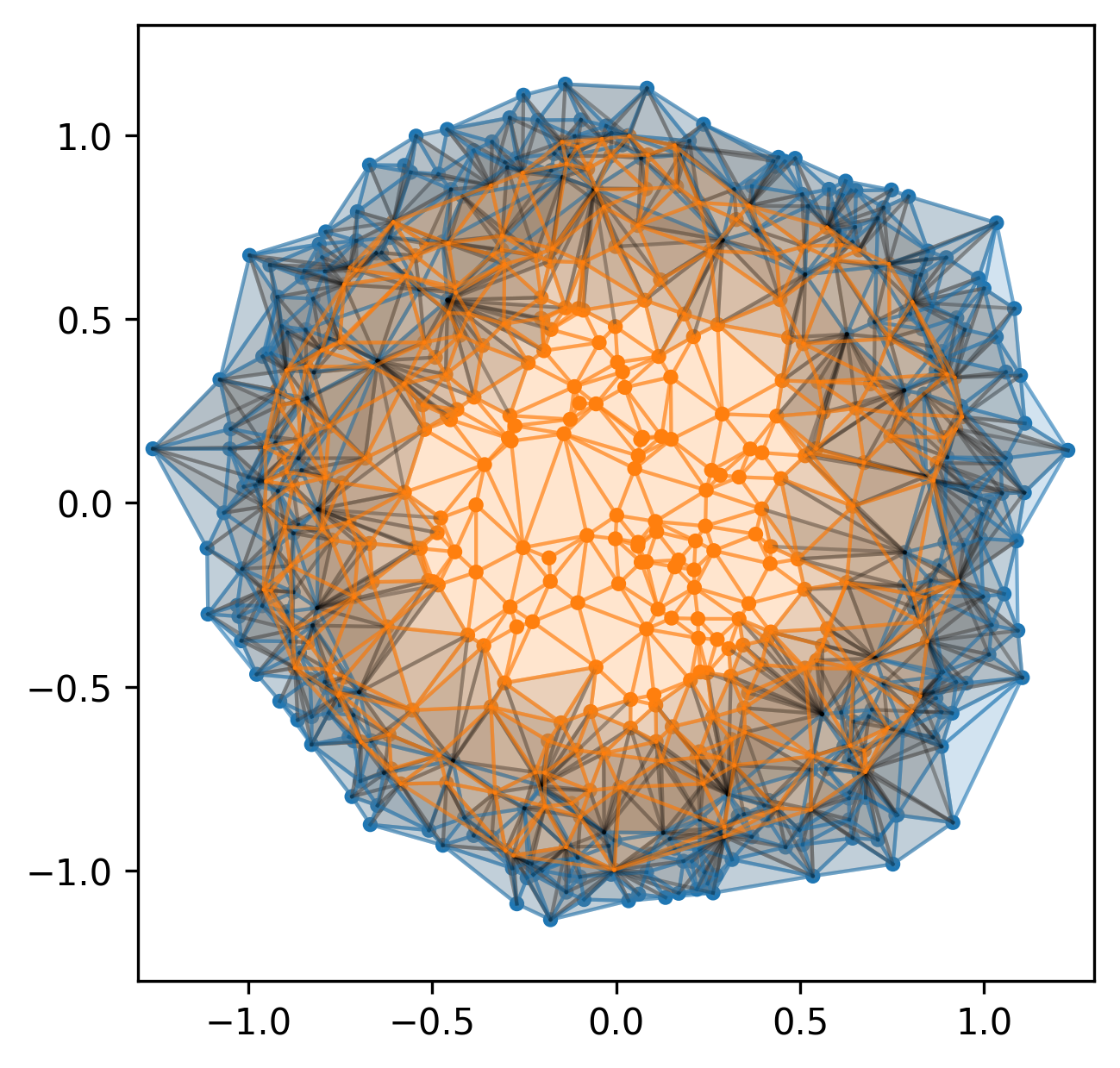
More generally, we can study the invariants of these induced maps to quantify the spatial relationships in our data.
Computational challenges
The Čech and Vietoris-Rips filtrations can be huge.
For very large datasets, we run into a wall with computational cost (especially memory).
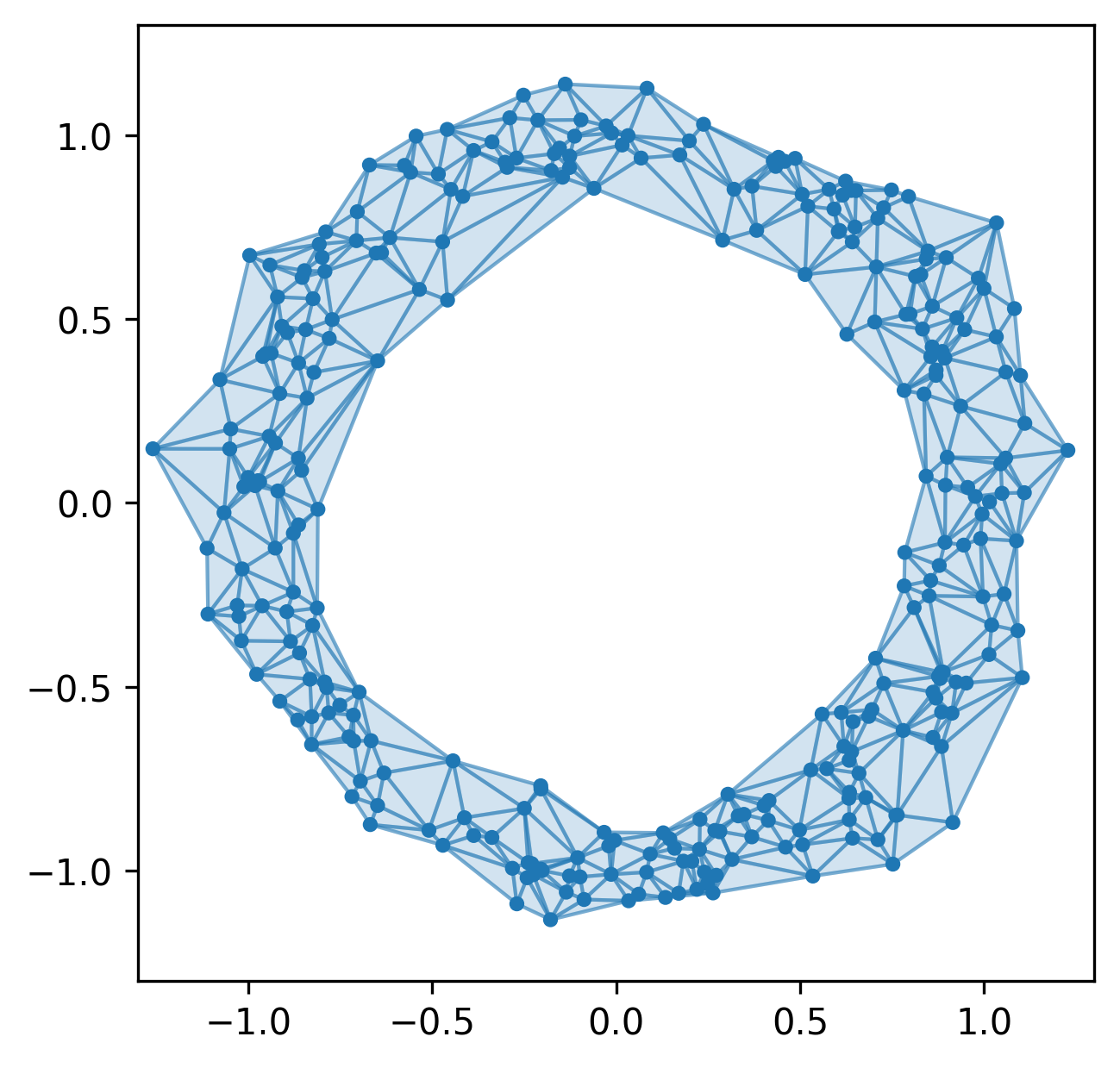
Alpha complexes
Filtration on a Delaunay triangulation that is much sparser than the Čech filtration … but not functorial with respect to inclusion of subsets of points.Chromatic alpha complexes
(S. C. di Montesano et. al., 2022).
the chromatic alpha complex is a filtered geometric simplicial complex A∙(X,χ).
For I⊂{0,…,s}, denote XI:=χ−1(I). Then:
- For I⊂J⊂{0,…,s}, the inclusion XI⊂XJ induces an inclusion A∙(XI,χ)↪A∙(XJ,χ). We have functoriality with respect to some inclusions of subsets. Chromatic alpha complexes interpolate between the Čech and alpha complexes (both of which are special cases).
- There is a filtration-preserving inclusion A∙(X,χ)↪Cˇ∙(X) that is a filtered homotopy equivalence ⟹A∙(X,χ) recovers spatial information.
- (Ranita Biswas et. al. 2022) Chromatic alpha complexes have O(n⌈2d⌉) cells for random colourings ⟹ practical in low-dimensions. If d=2 then they have at most O(s2n) cells.
Computing maps of persistence modules
Given a map of persistence modules f∙:A∙→B∙, in general there is no nice algebraic description of f unless A and B have fewer than 4 time steps, or no nested bars (E. Jacquard, 2016).
Algorithms are available to compute ker(f),coker(f), and im(f) (Cohen-Steiner et. al., 2009).
If f:A→B is induced by some inclusion of complexes K↪L, then we can also compute H∗(L,K).
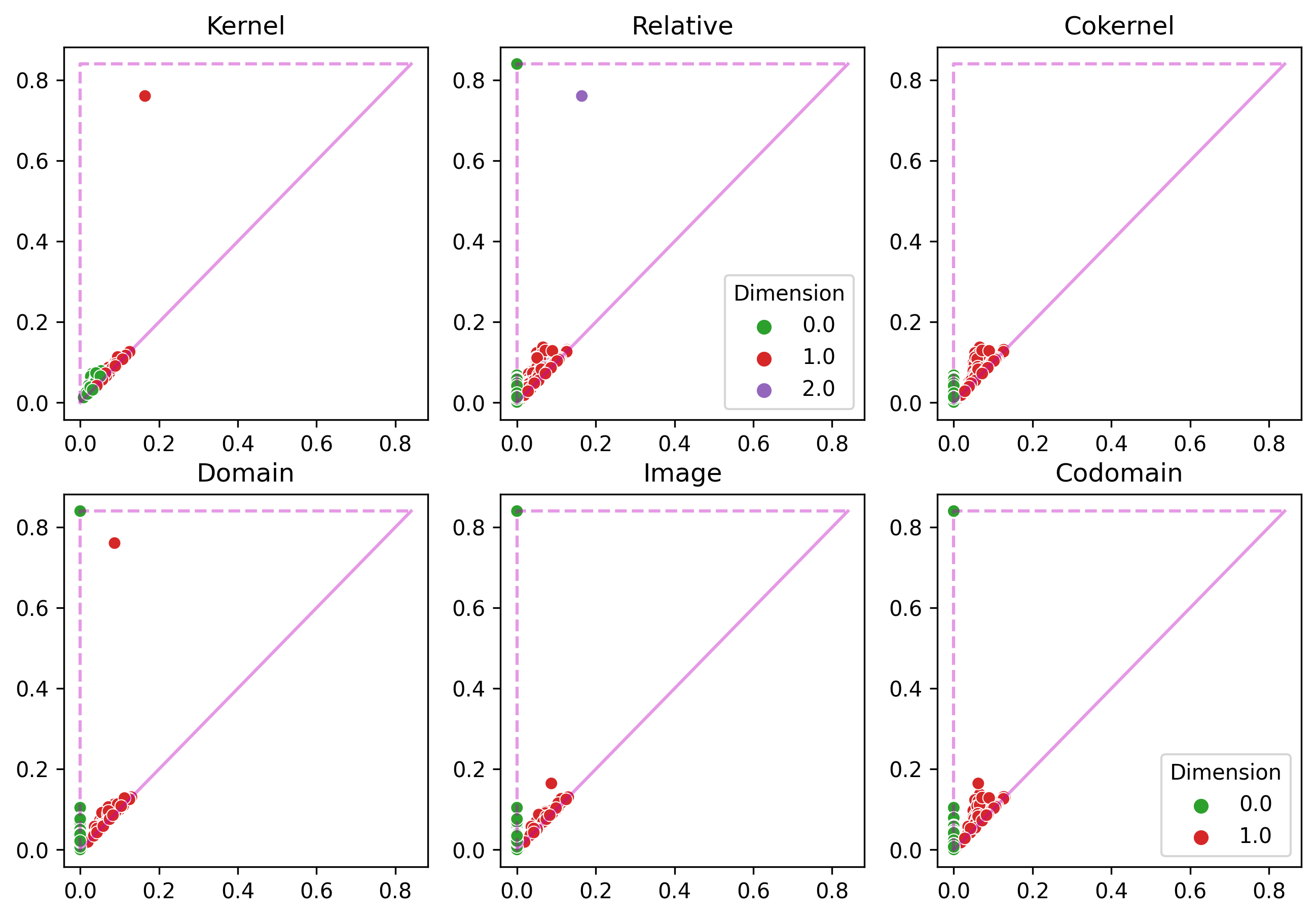
Six packs
Upshot: for each inclusion of subsets of points ⟹ obtain 6 persistence diagrams in each homological dimension.
Example 1
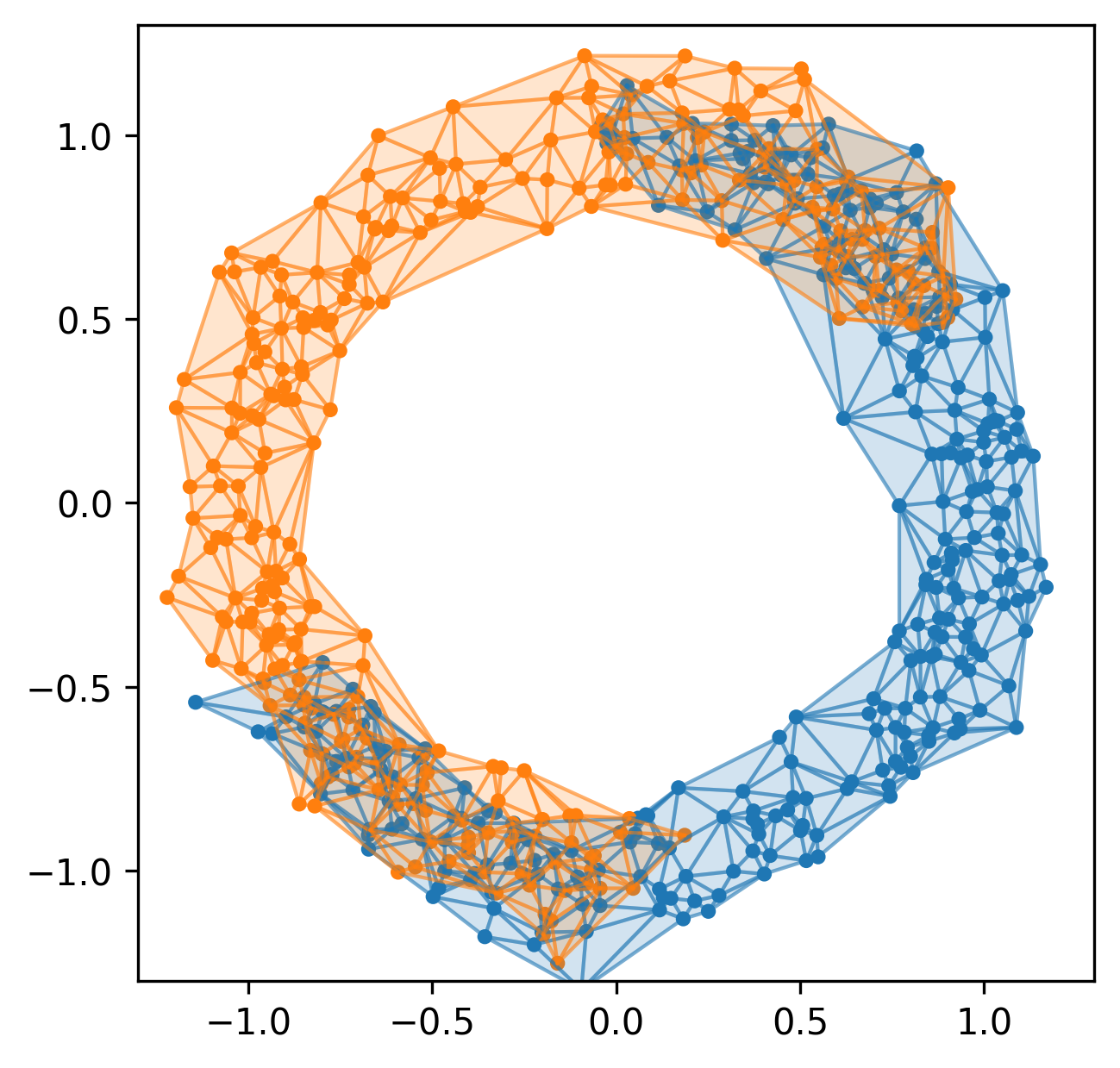
Example 2
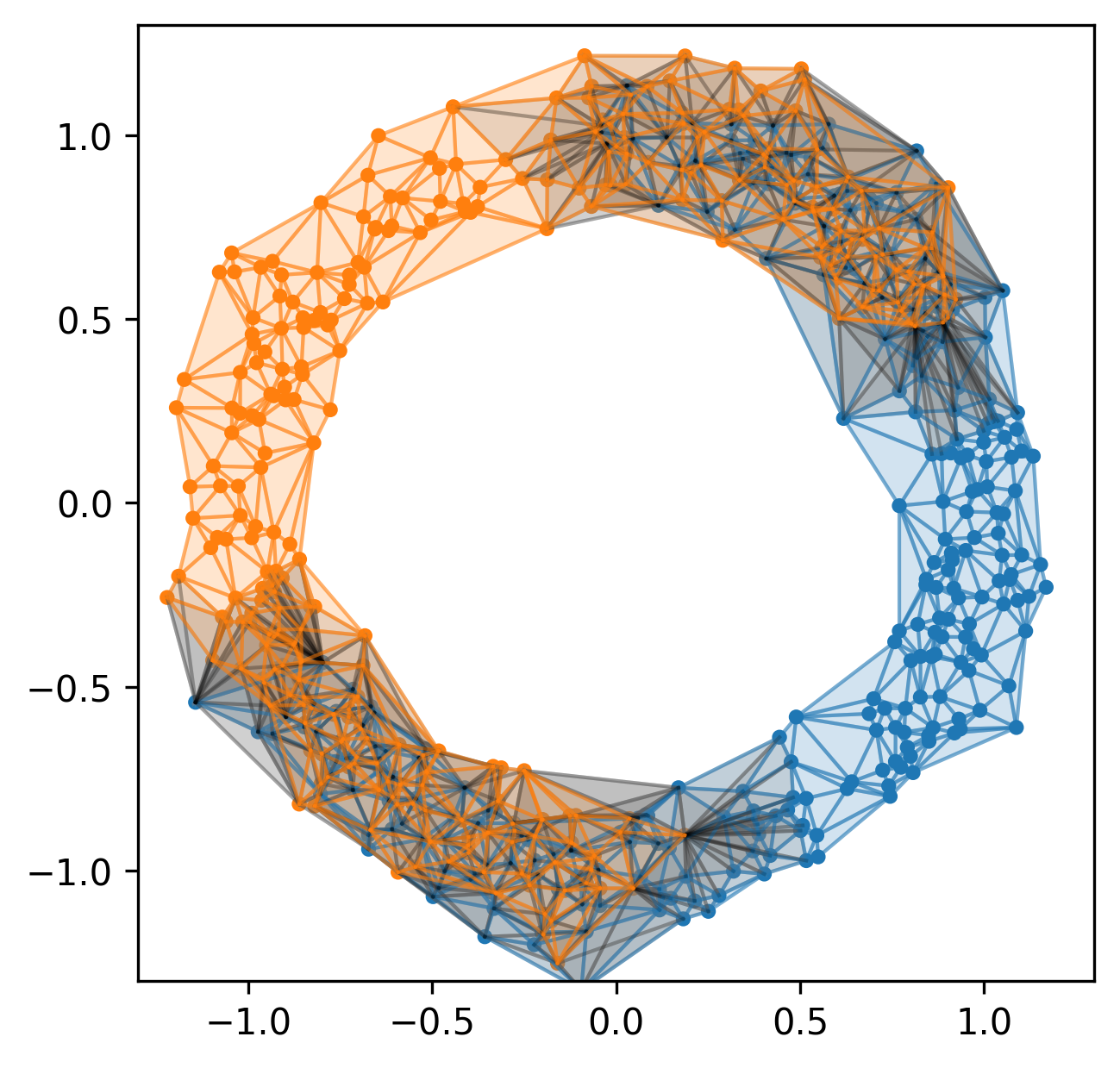
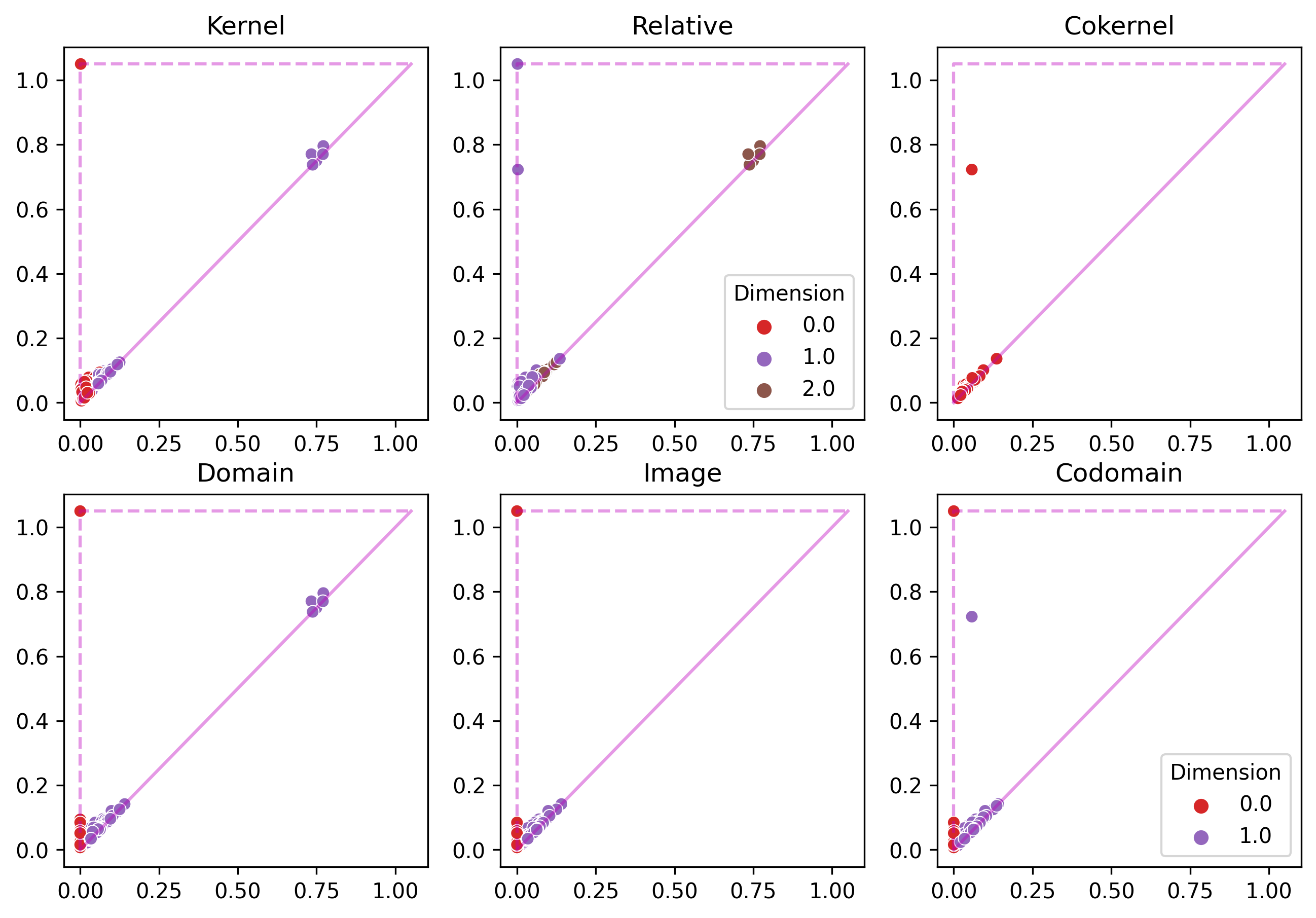
Current pipeline
- Find the most common cell-type pairs among all the samples
- Discard samples that do not have at least 3 of these cell-type pairs in them
- Compute the kernel, domain, and codomain diagrams in degrees 0 and 1
- Persistent statistics
- Scaling + PCA
- Classification (neural nets, random forests) into adenoma/carcinoma
- Achieve around 82% accuracy, baseline is 65%
Software
Soon to be released software for computational pipeline, including visualisation and statistics.
References
R. Biswas, S. C. di Montesano, O. Draganov, H. Edelsbrunner, M. Saghafian et. al. “On the size of chromatic Delaunay mosaics” (2022). DOI: 10.48550/arXiv.2212.03121
S. C. di Montesano, O. Draganov, H. Edelsbrunner, M. Saghafian. “Persistent Homology of Chromatic Alpha Complexes” (2022). DOI: 10.48550/arXiv.2212.03128
D. Cohen-Steiner, H. Edelsbrunner, J. Harer, D. Morozov, “Persistent homology for kernels, images, and cokernels” (2009) in “Proceedings of the twentieth annual ACM-SIAM symposium on Discrete algorithms”, Society for Industrial and Applied Mathematics.
E. Jacquard, V. Nanda, U. Tillmann, “The Space of Barcode Bases for Persistence Modules” (2023) J Appl. and Comput. Topology., 7(1) pp. 1-30.
U. Bauer, H. Edelsbrunner, “The Morse theory of Čech and Delaunay complexes” (2016) Trans. Amer. Math. Soc., 369(5) pp. 3741-3762.